リスク工学概論

モデリングによる現象の再現に内在するリスク

高安亮紀

2017年6月26日

モデリングとは

「現実の世界で起きるさまざまな問題を方程式などの数学的な形で表現すること」（ASCII.jpデジタル用語辞典）
「現象の動きを模倣する，微分方程式などの「数学の言葉で記述した系」のこと」（Wikipedia）
「現実の問題のある側面に注目し抽出された数学的分析・推論が可能な明晰な関係規則」（谷村省吾(名古屋大学), 物質情報学2の講義資料より抜粋）

現象（現実問題）を簡略化して表現する数式（数学問題）

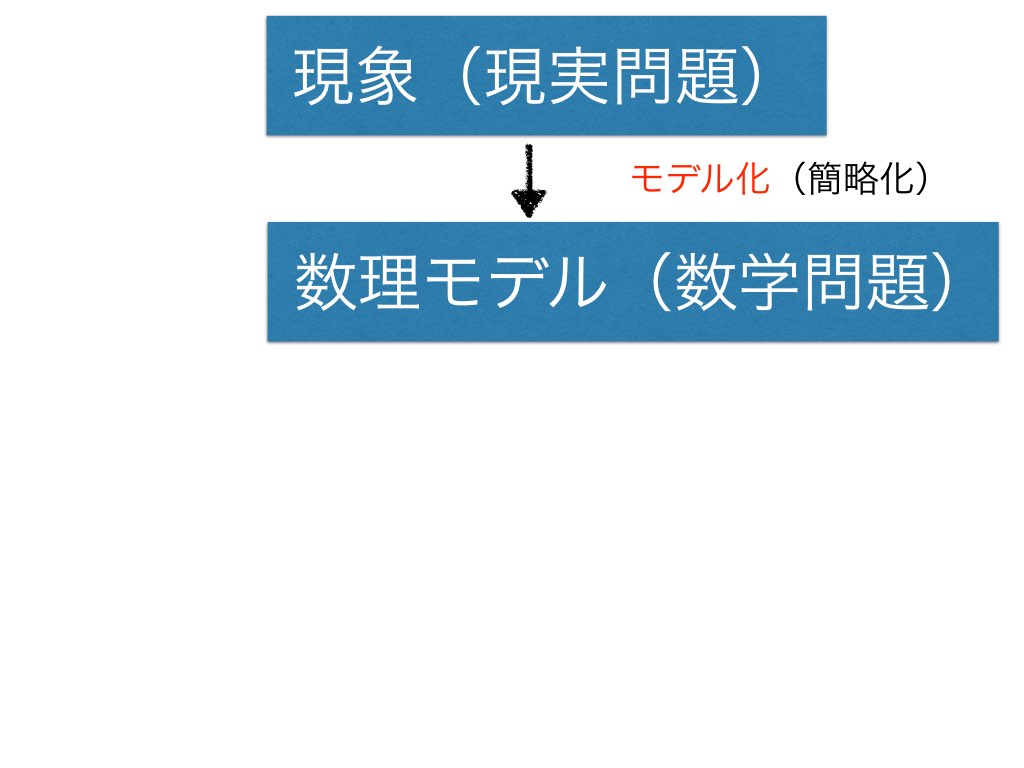
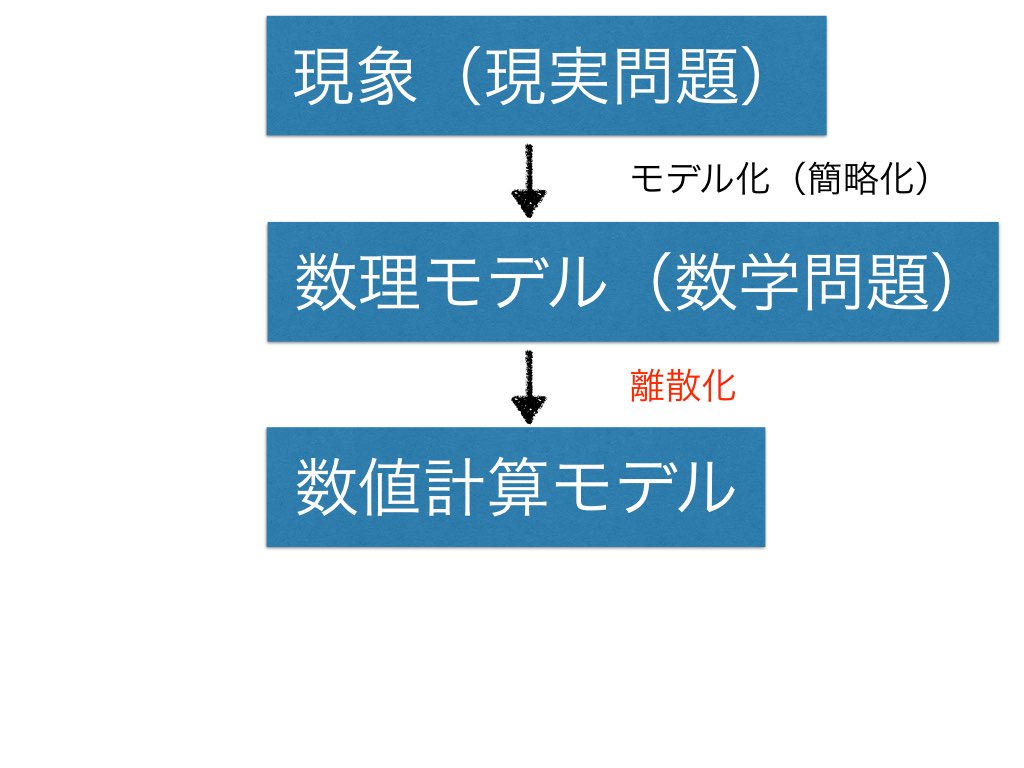
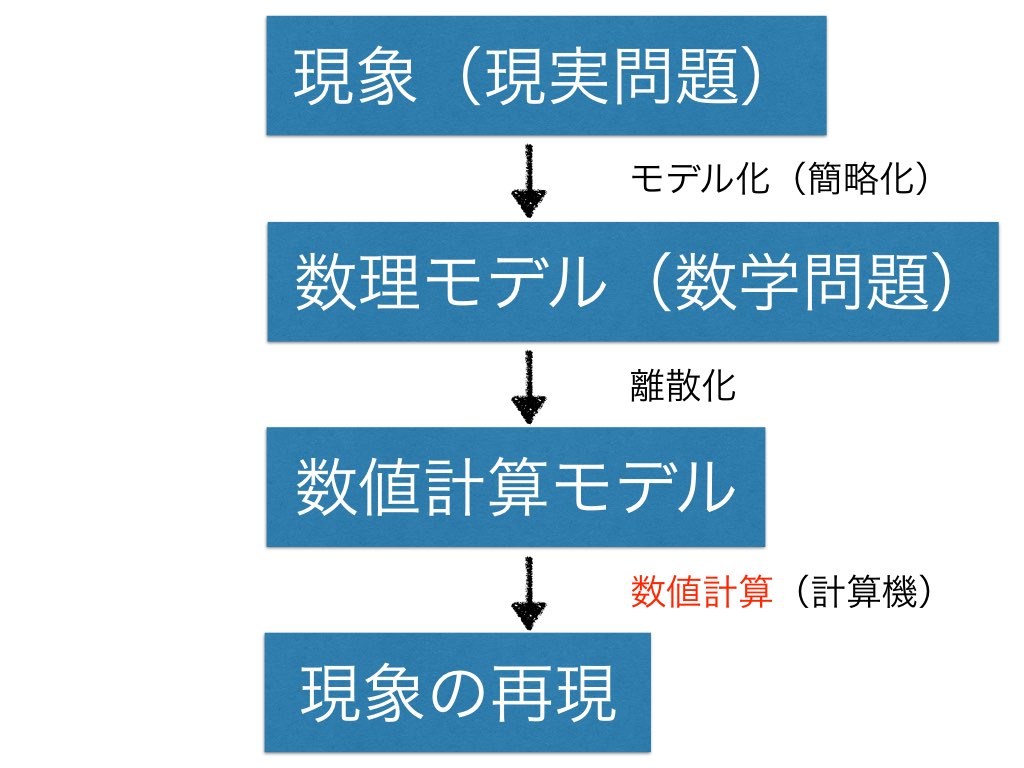
モデリングとは

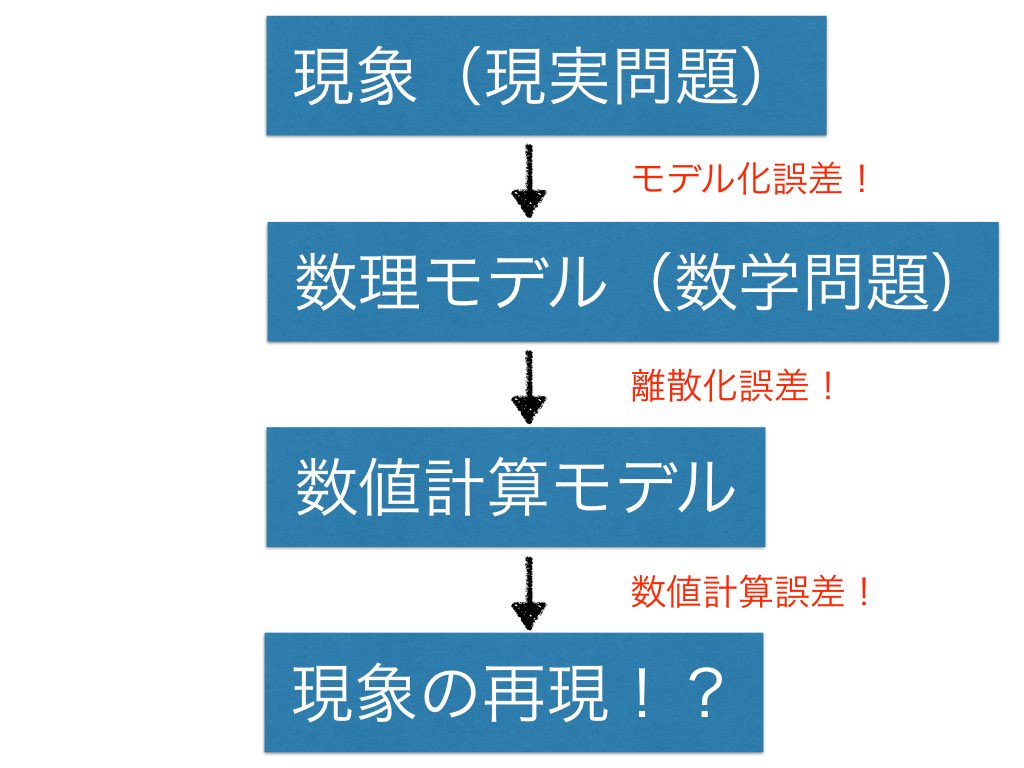
例（社会工学）マルサスの人口論 1798年

$N(t)$：人口を表す実数値関数（時間$t$の関数）,

人口の増加割合は現在の人口に比例するとすると

\[ \frac{dN}{dt}=aN~~~(a\in\mathbb{R}). \]

$a$は出生率マイナス死亡率.

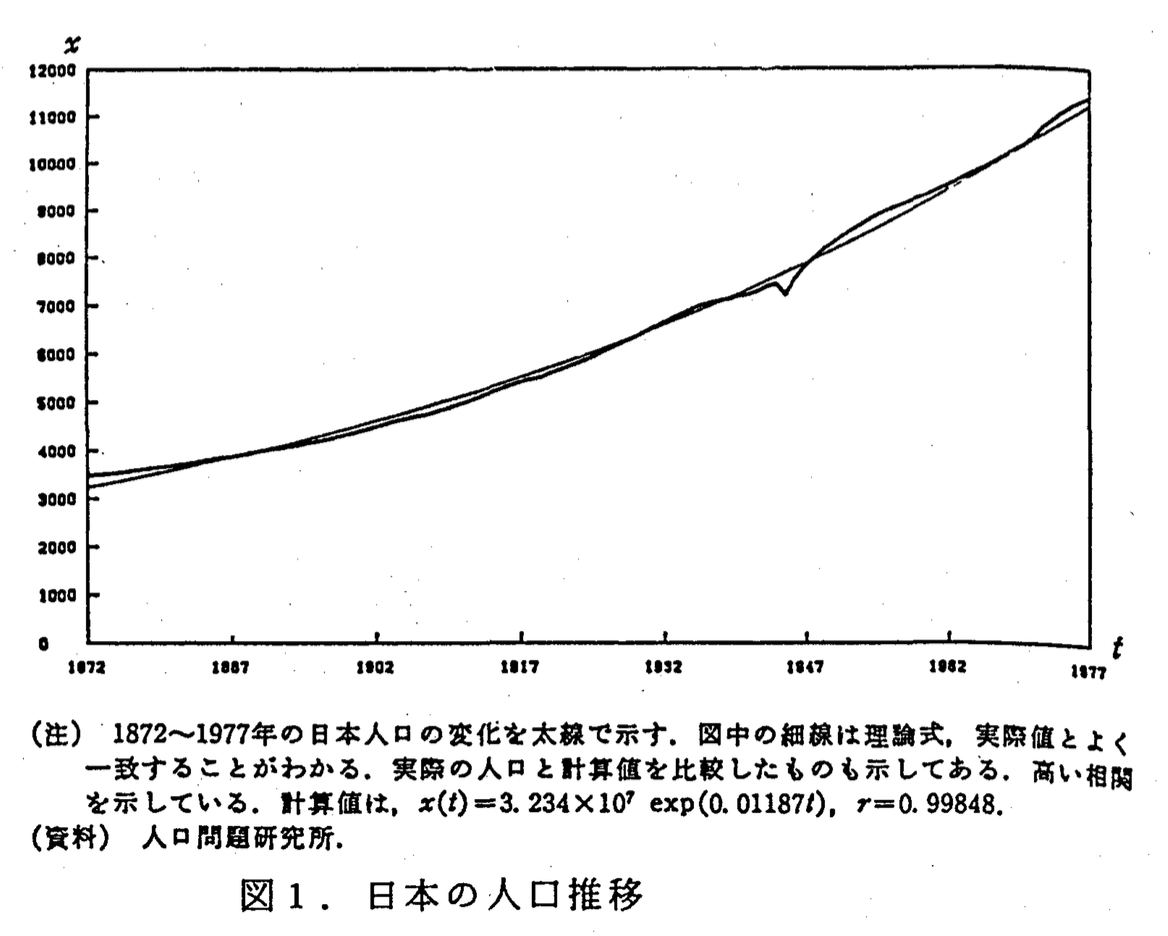
${}^1$近藤次郎, 現象と数理より抜粋

レイン-エムデン方程式

\[ \Delta u+u^p=0 \]

天体物理学，流体力学でのモデル方程式
星の密度分布を記述する
典型的な半線形楕円型偏微分方程式

この方程式をフーリエ・ガレルキン法で数値計算してみる

$p=2$, $\Omega=(0,\zeta)\times(0,1/\zeta)$, $\zeta=2.9$ として

$x\in\partial\Omega$ 上で $u=0$（Dirichlet境界条件）を課すと…

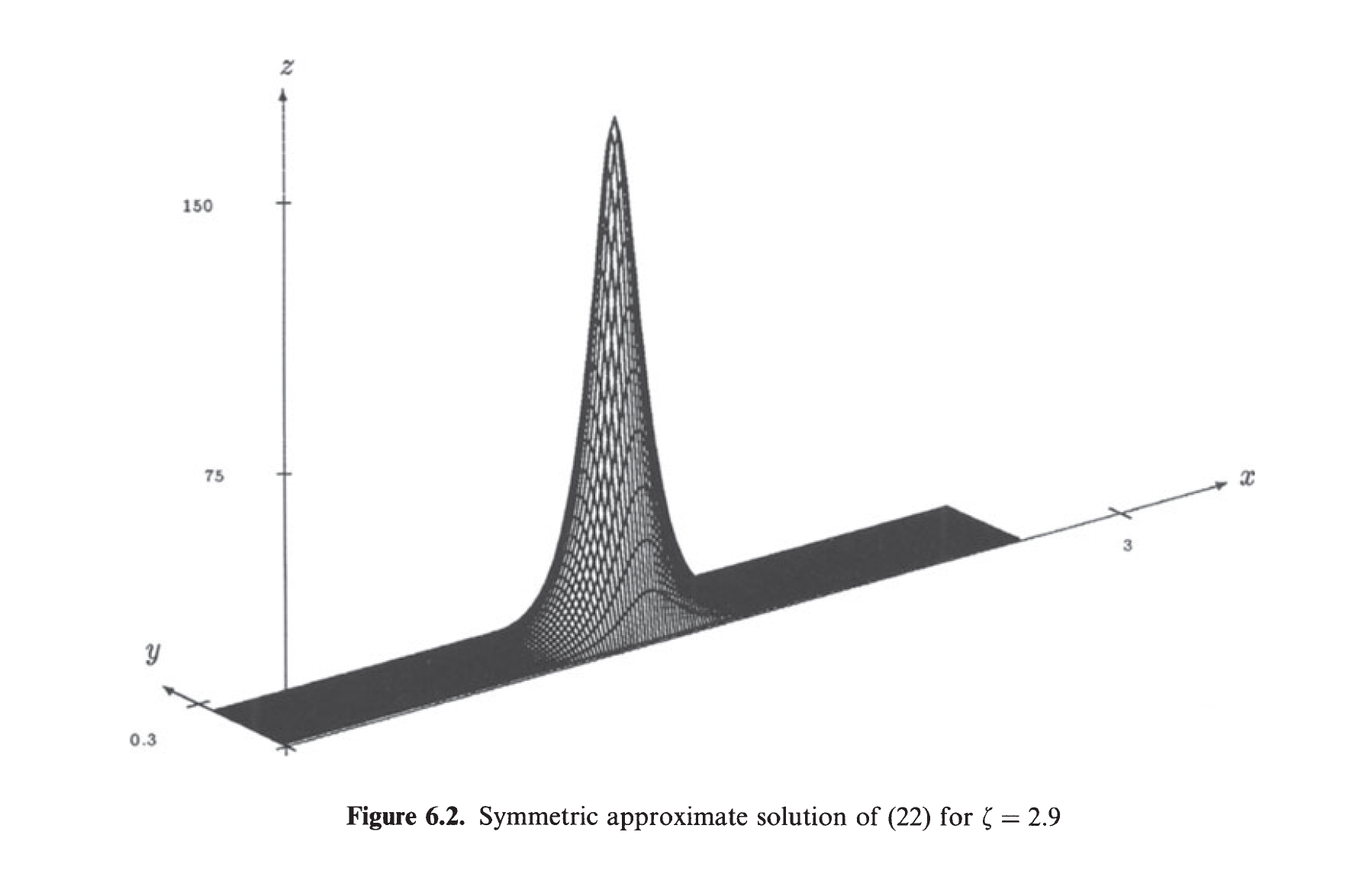
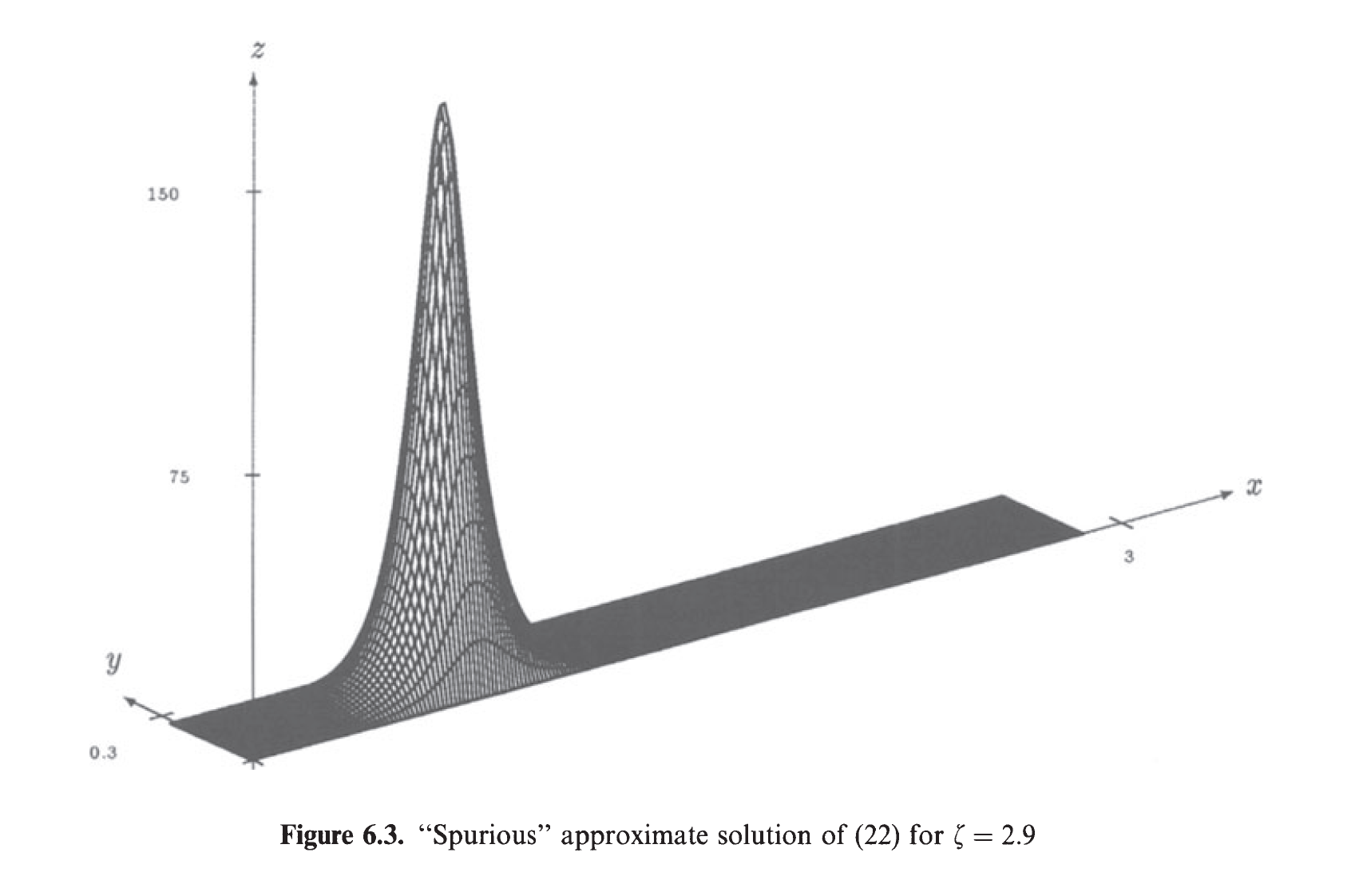
B. Breuer, M. Plum and P.J. McKenna: Inclusions and existence proofs for solutions of a nonlinear boundary value problem by spectral numerical methods, Comput. Suppl., 15, 61-77 (2001).

非線形問題なので解がいくつもあるのはよくある事
フーリエ・ガレルキン法は高精度
数値計算によって現象を再現できた！

しかし

解の一意性に関する数学理論に反する！！

B. Gidas, W.-M. Ni and L. Nirenberg: Symmetry and related properties via the maximum principle, Comm. Math. Phys., 68(3), 209-243 (1979).

上記論文によれば，$\Omega$ の中心に対して対称な解しか持たない．すなわち

こんな解は本来あってはならない解！

何が起きた？

B. Breuer, M. Plum and P.J. McKenna: Inclusions and existence proofs for solutions of a nonlinear boundary value problem by spectral numerical methods, Comput. Suppl., 15, 61-77 (2001).

では数理モデルを離散化した際の誤差（離散化誤差）が引き起こした間違いだと指摘．

つまり，一般的に高精度な解法だからといってむやみやたらに適用すると，思いがけない間違いを引き起こしてしまうリスクが内在してしまう事になる．

どう対処する？

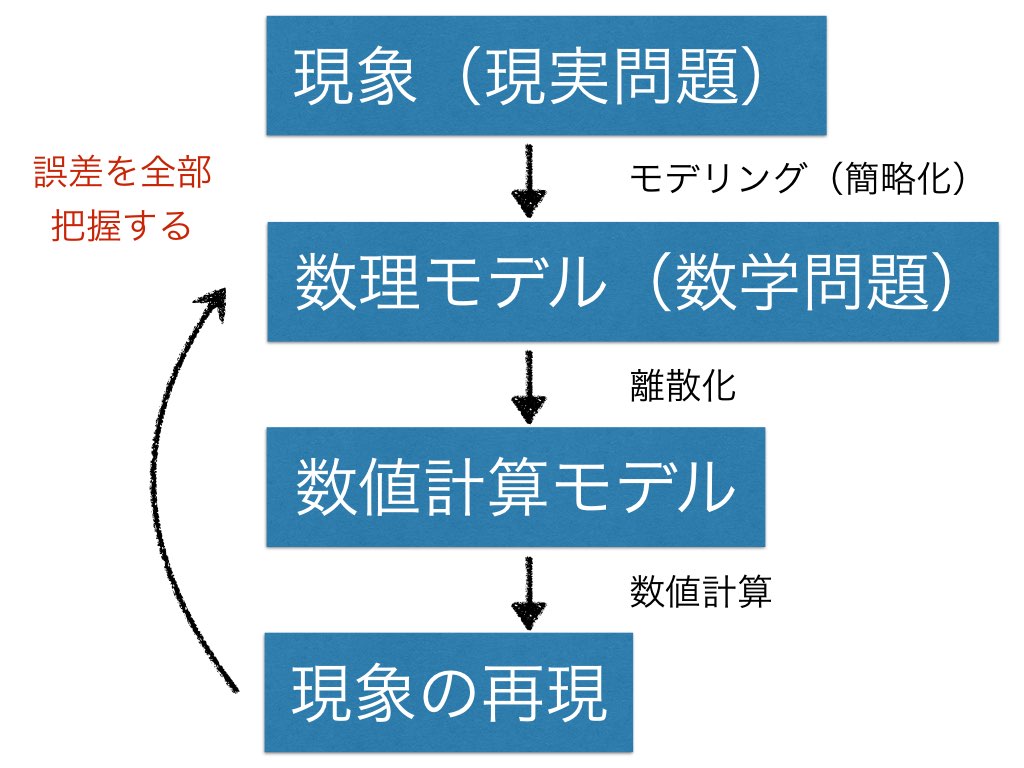
精度保証付き数値計算

$V$ をあるヒルベルト空間，$V^*$ を $V$ の共役空間とする
$\mathcal{F}:V\to V^*$をある非線形作用素とするとき，楕円型偏微分方程式は次のような問題になる

\[ \mbox{Find}~u\in V~\mbox{such that}~\mathcal{F}(u)=0~\mbox{in}~V^*. \]

Ex.

\[ \Delta u+u^p=0\iff\int_\Omega\nabla u\cdot\nabla v dx-\int_\Omega u^pvdx=0,~\forall v\in V, \] \[ \mathcal{F}(u):=\int_\Omega\nabla u\cdot\nabla v dx-\int_\Omega u^pvdx,~\forall v\in V. \]

定理（Newton-Kantorovich）

$\hat u$ を $\mathcal{F}(u)=0$ の近似解とし，$\mathcal{F}$ の $\hat u$ におけるFréchet微分を $\mathcal{F}'[\hat u]$ とする．もしも $\mathcal{F}'[\hat u]$ が可逆で，

\[ \|\mathcal{F}'[\hat u]^{-1}\mathcal{F}(\hat u)\|_{V}\le\alpha \]

をみたし，さらに開集合 $D\supset B(\hat u, 2\alpha)=\{v\in V:\|v-\hat u\|_{V}\le 2\alpha\}$ に対して，

\[ \|\mathcal{F}'[\hat u]^{-1}(\mathcal{F}'[v]-\mathcal{F}'[w])\|_{V,V}\le\omega\|v-w\|_{V},~\forall v,w\in D \]となるとする．このときもし $\alpha\omega\le1/2$ ならば解 $u^* \in V$ が存在し， \[ \|u^*-\hat u\|_{V}\le \rho:=\frac{1-\sqrt{1-2\alpha\omega}}{\omega}. \] をみたす．さらに $u^*$ は $D$ において唯一解となる．

3つの値を評価するだけ

線形化逆作用素のノルム評価：

\[ \|\mathcal{F}'[\hat u]^{-1}\| _{V^*,V}\le C_1, \]

近似解の残差評価：

\[ \|\mathcal{F}(\hat u)\|_{V^*}\le C_{2,h}, \]

Fréchet微分のLipschitz定数評価：

\[ \|\mathcal{F}'[v]-\mathcal{F}'[w]\|_{V,V^*}\le C_3\|v-w\|_{V},~~~\forall v,w\in D\subset V. \]

このとき $C_1^2C_{2,h}C_3<1/2$ なら解の存在と一意性が計算機で証明できる．

先ほどの問題を適用してみると

線形化逆作用素のノルム評価：

\[ \|\mathcal{F}'[\hat u]^{-1}\| _{V^*,V}=\infty \]

つまり，非対称な解の存在が証明できない．

計算機を使って得た近似解に対して，何かおかしいな？と気づかせる事が可能．計算結果に嘘をつかない．

まとめ

数理モデルを用いた現象の再現には様々な誤差が入り込む
現象の再現性を確かめる事は従来人間の勘
時に重大な間違いをおかすリスクを含んでいる
誤差をすべて把握し，計算結果に注意を出す事ができる

参考文献

近藤次郎, 現象と数理（応用数理学会創設総会記念講演会, 設立総会および記念講演会）, 応用数理, 創刊準備第2号, 1990年, 18-33.
柳田英二, 反応拡散方程式, 東京大学出版会, 2015.
B. Gidas, W.-M. Ni and L. Nirenberg: Symmetry and related properties via the maximum principle, Comm. Math. Phys., 68(3), 209-243 (1979).
B. Breuer, M. Plum and P.J. McKenna: Inclusions and existence proofs for solutions of a nonlinear boundary value problem by spectral numerical methods, Comput. Suppl., 15, 61-77 (2001).
P. Deuflhard: Newton Methods for Nonlinear Problems, Springer-Verlag, Berlin, 2004.

課題

Newton-Kantorovichの定理は関数

\[f(x)=2x^3+3x^2-8x+3=0,~f:\mathbb{R}^1\to\mathbb{R}^1\]

に対しても有効である．近似解を $x=1.2$ としてNewton-Kantorovichの定理を適用し解の厳密な誤差評価 $\rho$ を導け．計算結果をPDFにしてManabaに提出せよ．

提出期限：7月3日